4. 근사적분과 도심 / 수정역학적 곡선

별이쿤 2022. 1. 20. 23:07

4.1.1 근사적분과 도심(centriod)

선도의 정면도로부터 각 스테이션에서의 횡단면적을 구한 후, 이를 길이방향으로 적분하면 배수용적과 배수량, 부심(center of buoyancy) 등을 얻을 수 있다. 또 반폭도로부터 만재 상태 및 각 흘수에서의 수선면의 면적과 도심을 얻을 수 있다. 이를 토대로 배의 다양한 수정역학적 특성 및 트림, 복원 성능 등을 구할 수 있다.

위에서 언급한 바와 같이 선박과 관련된 계산은 횡단면이나 수선면과 같이 수학적 곡선으로 나타내기 힘든 도형의 면적을 구하는 작업을 포함하는 경우가 많은데, 이런 작업은 보통 근사적분법을 사용하여 이루어진다. 가장 많이 쓰이는 근사적분법으로는 사다리꼴 공식, 심프슨의 공식(Simpson's rule) 등이 있으며, 필요한 값들을 얻기 위한 계산에는 대부분 전산기 및 전용 소프트웨어를 활용하고 있다. 아래에서는 사다리꼴 공식과 심프슨의 공식의 기본에 대해 간단히 설명하기로 한다.

1. 사다리꼴 공식(trapezoidal rule)

임의의 곡선 아래 면적을 구하는데 가장 쉽게 생각할 수 있는 근사방법은 면적을 구하고자 하는 주어진 구간(interval)을 잘게 자르고 각 소구간(subinterval) 내에서 곡선을 직선으로 근사하는 방법이다. 고등학교 때 적분의 정의와 관련해서 배운 바로 그런 방법인데, 단 이 방법을 실제적으로 계산에 이용할 때에는 소구간의 길이를 무한히 작게 할 수 없으므로 어느 정도의 오차를 감수해야 한다. 이 방법은 적용이 간편하지만 오차가 비교적 크며, 정확한 결과를 얻기 위해서는 소구간의 길이 h를 매우 작게 해야 한다는 단점이 있다.

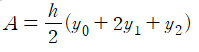
2. 심프슨의 공식(Simpson's rule)

심프슨의 공식은 사다리꼴 공식에 배해 소구간의 길이가 같을 때 오차가 작은 결과를 준다는 장점이 있다. 임의의 곡선을 위에서와 같이 직선으로 근사하는 것은 1차식으로 보는 것과 같은 것임에 착안하면, 보다 작은 오차를 얻기 위해 2차식, 다시 말하면 포물선으로 근사하면 어떨까 하는 생각을 할 수 있는데, 심프슨의 공식은 바로 그와 같은 가정에 근거하여 얻을 수 있다.

이 식의 우변이 심프슨의 공식으로 알려져 있으며, 근사적분 시 가장 많이 사용되고 있다. 면적을 구하고자 하는 구간을 2의 배수로 등분하여 위의 결과를 반복적으로 적용함으로써 비교적 정확한 결과를 얻을 수 있다.

3. 도심(centroid)

먼저 평면도형의 임의의 축에 대한 모멘트를 고려하기 위해 직각좌표계 xy를 잡고, 도형의 y축에 대한 모멘트 Mx를 정의하면 다음과 같다.

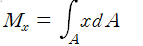
여기서 dA는 면적 요소(area element)이며 적분은 도형에 대한 면적 적분이다. 만약 도형과 y축 사이의 거리가 대단히 멀다면 위의 적분은 도형 내부 임의의 점에 대한 x의 값, 예를 들어 x0와 면적 A의 곱으로 보아도 그렇게 틀리지 않을 것이다. 그러나 도형과 y축 사이의 거리가 짧다면 이와 같은 방법은 x0의 값에 따라 매우 다른 결과를 줄 것이다. 만약 어떤 x0에 대해 위에서 생각했던 방법을 그대로 쓸 수 있다면 편리할 것이며, 그와 같은 경우는 x0는 다음과 같이 정의할 수 있다.

위 식은 평면도형의 도심의 x좌표를 주는 식이며, 도심의 y좌표 y0는 같은 방법으로 x축에 대한 모멘트를 고려하여 다음과 같이 얻을 수 있다.

위에서 보인 도심의 정의로부터 도심을 지나는 축에 대한 모멘트는 영이 됨을 보일 수 있다. 예를 들어 xy좌표계의 원점을 도심으로 옮기고 새로운 좌표계를 Zeta·Eta좌표계라고 하자. 이제 도형의 Eta 축에 대한 모멘트 Mzeta를 구하기 위해서는 위의 식에서 x를 Zeta로 바꾸면 되는데, Zeta = x - x0 임을 이용하면 다음과 같이 원하는 결과를 얻는다.

물론 같은 방법으로 Zeta 축에 대한 모멘트 Meta도 영이 됨을 보일 수 있다. 다시 말하면, 주어진 기하학적 형상의 도심은 '그 점에 대한 모멘트가 영이 되는 점'이라고 할 수 있다.

위에서 얻은 결과는 공간도형 즉 예를 들면 3차원 형상의 물체에 대해서도 그대로 확장 적용할 수 있으며, 도심의 근본적인 성질, '도심에 대한 모멘트는 영이다'라는 점은 그대로 성립한다.

4.1.2 수정역학적 곡선(Hydrostatic curves)

어떤 배든지 지금 흘수에서 배수량이 얼마나 되는지, 또 짐을 얼마나 더 실을 수 있는지에 대해 배를 운용하는 사람이 알 필요가 있으며, 이에 따라 조선소는 짓는 배의 수정역학적 특성, 다시 말하면 배가 움직이지 않고 정지 상태에 있다고 가정할 때, 배의 특성을 선주에게 제공할 의무가 있다. 여기서 특성이라고 함은 흘수가 달라질 때 변화하는 여러 가지 양들을 뜻하는데, 배수량, 부심의 위치, 부면심의 위치, 메타센터의 위치, 단위침하당(per unit immersion) 배수량 변화, 단위 트림당(per unit trim) 모멘트, 침수표면적, 선형계수 등이 포함된다. 물론 이와 같은 배의 특성은 배를 설계, 건조하는 과정에서도 꼭 필요한 양이다. 아래에서는 이들 양에 대해 차례로 보다 자세히 알아보기로 한다.

1. 배수량

배수량은 중량이므로 배수용적을 구한 후, 배가 떠있는 물의 비중을 곱하여 얻어지는데, 물의 비중은 해수, 담수에 따라 달라지고 또 계절(온도), 지구 상의 위도에 따라서도 달라지므로 주의를 요하며, 대개 하계 해수를 기준으로 작성한다. 주어진 흘수에서의 배수량을 구하기 위해서는 근사적분을 사용하며 보통 전용 소프트웨어를 이용한다.

2. 부심

부력은 힘, 즉 벡터량이므로 크기, 방향, 작용점을 가진다. 아르키메데스의 원리에 따라 부력의 크기는 배수량과 같고 그 방향은 연직 상방이며, 부력의 작용점은 물에 잠긴 부분의 도심이 되는데, 이 점을 부심이라고 하며 점 B로 표기한다. 따라서 부심, 즉 해당 도형의 도심을 구하기 위해서는 해당 체적과 체적의 모멘트를 알아야 되며, 이 양들은 모두 위에서 설명한 근사적분으로 얻을 수 있는 양들이다.

배가 수평상태(even keel)로 떠있을 때는 부심은 당연히 중앙종단면 내에 있으며 따라서 부심의 위치는 길이방향, 수직방향의 좌표로 주어진다. 부심의 길이방향 위치는 종방향(Longditudinal Center of Buoyancy, LCB)이라고 부르며, 기준면으로는 중앙횡단면을 택하고 배의 길이에 대한 백분율(%)로 나타내는 것이 일반적이다. 수직방향 위치는 통상 기선으로부터의 수직거리로 주어지며 KB로 표시한다. 여기서 점 K는 중심선과 기선의 교점으로 정의되고, K는 기선이 용골(keel) 상면으로 정의되는 것을 나타낸다.

3. 부면심(center of floatation)

해당 흘수에서의 수선면(water plane)의 도심을 부면심이라고 하며, 근사적분을 이용하여 구할 수 있다. 부면심 또한 수선면의 좌우 대칭성 때문에 중심선 상에 있고 따라서 부면심의 위치는 길이방향 위치를 뜻하며 통상 LCF(Longditudinal Center of Floatation)로 표시한다.

4. 메타센터(metacenter)

정적복원성과 관련하여 매우 중요한 개념인데, 배가 횡방향으로 기울면 부심의 위치는 중앙종단면을 벗어나게 되며, 이때 새로운 부심을 지나는 수직선은, 흘수가 변하지 않고 경사각도가 작은 한, 중앙종단면 또는 중심선과 항상 동일한 점에서 만나게 된다. 이 점을 횡메타센터(transverse metacenter)라고 하며, 물론 배가 종방향으로 기우는 경우에 대해서는 같은 방법으로 종메타센터(longditudinal metacenter)를 정의할 수 있다.

횡메타센터는 통상 'M'으로 표시하며 따라서 KM은 점 K와 횡메타센터 사이의 거리를 뜻한다. 종메타센터는 ML로 표시한다. 배의 경우 횡방향으로 기우는, 즉 횡경사(heel)가 크게 일어날 때는 전복의 위험이 크지만 종방향으로 기우는, 즉 종경사(trim)가 크게 일어날 때는 상대적으로 큰 위험이 없으므로 보통 경사라고 하면 횡경사, 메타센터라고 하면 횡메타센터를 뜻한다.

KB는 위에서 부심과 관련하여 이미 설명한 바와 같이 구할 수 있으며, 배의 중심선 상에서 KM=KB+BM이므로 BM을 구하면 KM을 얻을 수 있다. BM은 메타센터 반경(radius of metacenter)이라고 부른다.

5. 단위침하당 배수량(Tons Per Centimeter immersion, TPC)

흘수의 크기가 단위길이(cm 또는 in) 증가할 때 배수량의 증가는 그 흘수에서의 수선면적에 단위 길이와 물의 비중을 곱하여 얻을 수 있으므로, TPC는 수선면적과 비례하는 양이다.

6. 단위트림당 모멘트(Moment to change 1 Centimeter Trim, MCT)

배가 종방향으로 경사하면 선수흘수와 선미흘수의 차이가 생기며 이를 트림이라고 하는데, 단위길이의 트림을 발생시키는데 필요한 모멘트(횡방향 축에 대한)는 종메타센터반경과 배수량의 곱을 배의 길이로 나눈 양에 비례함을 보일 수 있다.

7. 침수표면적(wetted surface area)

각 스테이션에서 점 K로부터 선체 표면을 따라 잰 길이, 즉 거스 길이(girth length)를 배의 길이방향으로 적분하여 얻을 수 있다. 침수표면적은 형배수량에서 제외되었던 외판에 기인하는 배수량을 고려할 경우 필요하며, 또한 저항의 무차원화에도 사용되는 양이다.

8. 선형계수(ship form coefficients)

앞서 설명한 선형계수들은 대부분 만재흘수에 대하여 정의되었지만 임의의 흘수에 대해서도 같은 방법으로 이들 선형계수를 정의하여 흘수의 함수로 계산할 수 있으며, 이들을 수정역학 곡선에 포함시키기도 한다.